Disclaimer: use at your own risk
© Stelling Consulting, 2008-2024 

Transportation problem solvers • Network minimum cost flow problem solver • Linear Programming problem solver

This web app solves transportation/network flow/LP problems with the Simplex method. The transportation problem can also be solved with problem-specific methods - Vogel's approximation + MODI + Stepping Stone - that solve 50-100 times faster than the Simplex method. Enter your input in the textarea below, and press Solve. Or use the Excel interface.
Download Excel interface   (45kB - downloaded 808 times)

 
 
Solve with Simplex
Solve with Vogel+MODI+Stepping Stone
 
Top-left cell = MIN       1st row = supply       1st column = demand       All other cells = transport cost per quantity
In this case, demand should be met by supply against minimal transportation costs. The table below shows demand, supply and the transportation cost per quantity for each supply-demand connection. Note that total demand equals total supply (no requirement as such). With r referring to row, and c to column, and Xrc to the transport quantity from Supplyr  to Demandc, and Crc to the transport cost per quantity from Supplyr  to Demandc the LP problem can be formulated as:

Minimize Σ Crc × Xrc   , subject to
Σ Xrc ≥ Demandc ∀ c
c

Σ Xrc ≤ Supplyr ∀ r
r

Xrc ≥ 0 ∀ r,c

Demo data

COST PER
QUANTITY		 SUPPLY
141516189471520232
DEMAND4033435633618457955929189585
14285234805283440325957330796600
26431965600241190417117916631436
18763719550396200619689514108874
10484933792607322548851715802272
3081661122579851425841481500903
1889939116515565723175773048282
892232066138726760150891483407
4316504123587938706382729547310
675137825754140323229592571914
6117706414674275703395315115891
12498898858498187411717353560368
18169470643433132652898719555444
2840336860577112292422294411474
2093556944363952354960415409791
32753614610426136578118335751494
208357210857024194665176279040
3616783896329936290843395045
2851765791479678811173364930593
2746440747392946456560462798462

Optimal quantities: total costs are 102587

OPTIMAL
QUANTITIES		 SUPPLY
141516189471520232
DEMAND40492223
14194
2626
1818
1010
301614
1818
88
44
66
66
1212
18711
22
20713
3232
2020
3636
2828
22
Add network problem specifics to the solution
Solve with Simplex
Enter data tab separated (copy-paste from Excel file) or semicolon separated.

Nodes

 NodeID  |  Supply_Min*  |  Supply_Max*  |  Costs_In  |  Costs_Out  |  Throughput_Min  |  Throughput_Max
* Supply >0 = supply node, <0 = demand node, 0 = balanced througput node

Arcs

 ArcID  |  From_NodeID  |  To_NodeID  |  Costs  |  Flow_Min  |  Flow_Max

Intro

You can define a netwok consisting of nodes and arcs. The decision variables in this type of problem are the arc quantities. Each arc has a cost per quantity (e.g. transportation costs), a lowerbound (minimum flow quantity) and upperbound (maximum flow quantity). Each node has supply quantity (demand = negative supply).

Demo case

The graph below shows a minimum cost flow problem. The arcs are labeled with pairs of numbers: the first number is the capacity and the second number is the cost. The number in parentheses next to a node represent supply or demand. Node 0 is a supply node that supplies 20, while nodes 3 and 4 are demand nodes (or: sink nodes) that demand 5 and 15 respectively (demand = negative supply).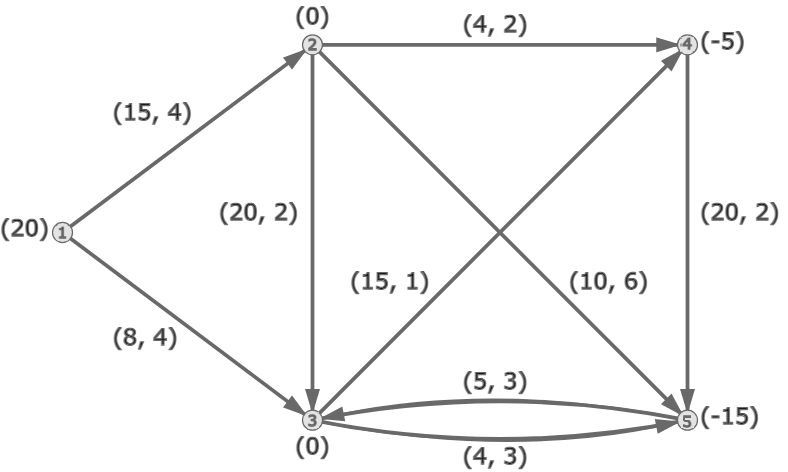

Advanced node modeling options

For modeling convenience this web app offers advanced node modeling options:
  • Each node has a cost per incoming and outgoing quantity (e.g. inbound and outbound warehouse handling costs).
  • Each node has flexible supply/demand (supply upper and lowerbound), so - for example - a node may supply between 0 and 1000, or have a demand between 6 and 10 (entered as a negative supply between -10 and -6). If demand/supply is not flexible, then enter the same value for both Min and Max.
  • Each node has a throughput upper and lowerbound. Throughput could be either based on incoming or outgoing quantity. We have (arbitrarily) chosen incoming quantity as the basis.

General network modeling remarks

  • By adding dummy nodes and arcs you can create completely balanced systems, and make a model 'better readible'.
  • Other network flow software may not offer advanced node modeling options.
    • You can create node upper and lowerbounds by splitting a node in two nodes, adding a zero costs arc in between, and setting upper and lowerbound at this arc (connecting all original incoming arcs to the first node, all original outgoing arcs to the second).
    • You can create a node with flexible demand/supply by adding a dummy node that 'eats' any non-used over-supply at zero costs (creating a balanced system in which total supply equals total demand).
    • Incoming/outgoing node costs can be transferred/added to all incoming/outgoing arcs of the node.
  • A network model can be used to model transitions in time, with an arc representing a transition from time to time+1.

Remark: Min(imum) and Max(imum) are called Lowerbound (LB) and Upperbound (UB) in LP terminology.
Solve with Simplex
Enter data tab separated (copy-paste from Excel file) or semicolon separated.
LP problem input = Simplex tableau. The format is explained below the text area.

Standard LP problem formulation

Maximize ΣCi × Xi   , subject to Σ (Aij × Xi) ≤ Bj ∀ j , and Xi ≥ 0 ∀ i
i
i
You can also minimize and/or use ≥ and = as restriction type as shown by the demo cases. See also: wikipedia: Linear Programming

Simplex tableau legend

  • Top row contains the cost factors.
    • 1st cell = MIN (minimize) or MAX (maximize). MIN is default in logistics. Though the standard LP problem formulation is about maximizing profit (MAX), logistics problems are usually about minimizing costs (MIN).
    • 2nd cell = initial goal value = always 0.
    • 3rd and next cells = costs factors Ci. Each of these column 'belongs to' one decision variable (X_1, X_2,...).

  • All other rows formulate the constraints.
    • 1st cell = constraint type <= or >= or =
    • 2nd cell = constraint value Bj
    • 3rd and next cells = values of Aij (optional: can be left empty if zero). Each of these columns 'belongs to' one decision variable (X_1, X_2,...)

Normally you need to setup - so called - slack variables as well (read: dummy variables required for the Simplex method to work). Do not enter slack variables! They are created automatically.
The tableau is prefilled with the transportation problem demo case. Putting the demo case table next to this Simplex tableau you will recognize the numbers. Note that instead of Xrc (20 rows × 10 columns) all has been translated into Xj (200 variables sitting on a single row), so Xr=6,c=3 has become X53 that has a value of 16 in the optimal solution. If you run "Solve network minimum cost flow problem" the tableau is filled with the translation of the network flow problem demo case.
 
The solution will appear here, once run.